
전에 풀었던 11726번 (2*n 타일링) 문제에 2 * 2 타일이 추가된 문제이다.
백준 11726번 : 2*n 타일링
2 * 1 크기일 경우 1개 2 * 2 크기일 경우 2개 2 * 3 크기일 경우 3개 2 * 4 크기일 경우 5개 이 문제를 해석해보면 결국, 피보나치수열임을 알 수가 있다. import java.util.*; public class Main { pub..
dyii.tistory.com
어떻게 풀어야하나 막막해서 다른 사람의 풀이 방법을 참고해서 다시 해석해보았다.
1. n : 1개
- 2*1 타일이 하나만 놓일 수 있다.
2. n : 2개
- 1*2, 2*1, 2*2 모두 한 번씩 총 3번 놓을 수 있다.
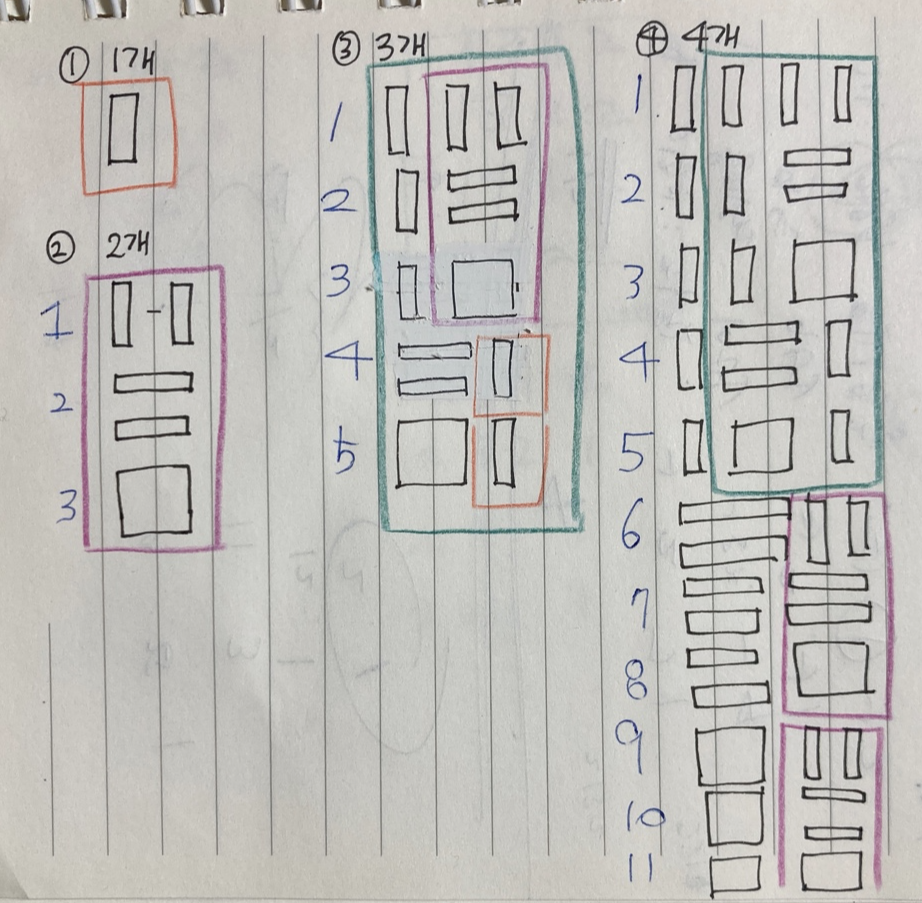
3. n : 3개
- 그림을 보면 알 수 있듯이 보라색 사각형 안에 있는 방법들이 n이 2일 때 방법들의 경우이며,
주황색 표는 n이 1일 때 방법들로, 타일에 1*2 타일과 2*2 타일에 대한 경우의 수가 합해진 것임을 알 수 있다.
이렇게 나오는 이유는
n번째 타일의 개수는 n-1번째 타일을 놓는 방식에 각각 2*1 타일( | )을 하나 추가할 수가 있고, 결국 맨 앞에 2 * 1 타일 ( | )을 놓는다고 생각하고 n-1번째 타일을 놓는 경우의 수를 그대로 가져올 수 있다.
하지만, n-1 번째 타일을 놓는 방식에서 2*1 타일( | ) 을 제거하면 1*2 ( -- ) 타일이나 2*2 타일 ( ㅁ ) 을 추가할 수 있다.
이 말은 결국 n-2 번째 타일을 놓는 방식에서 1*2 타일 ( -- ) 을 늘리거나, 2*2 타일 ( ㅁ ) 을 하나 추가하는 방법이 각각 늘어날 수 있음을 의미한다.
그러므로 식을 세워본다면 arr[n] = arr[n-1] + 2 * arr[n-2] 임이 유추가 된다.
4. n : 4개
- 초록색 사각형 안에 들어있는 저 경우의 수는 n이 3일때 방식이 그대로 들어감을 알 수 있다.
그리고 밑에 있는 보라색 사각형 안에 들어있는 경우의 수는 n이 2일 때 방식으로 1*2 타일 ( -- ) 과 2*2 타일 ( ㅁ ) 두 가지 경우가 있기 때문에 보라색 사각형은 2개가 된다.
식에 대입해보면 arr[4] = arr[3] + 2 * arr[2] = 5 + 2*3 = 11 로 답이 나옴을 알 수 있다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n = sc.nextInt();
int arr[] = new int[n+2];
arr[0] = 0;
arr[1] = 1;
arr[2] = 3;
for(int i=3;i<=n;i++) {
arr[i] = (arr[i-1]+arr[i-2]*2)%10007;
}
System.out.println(arr[n]);
}
}
'CS > 알고리즘' 카테고리의 다른 글
| 백준 14196번 : 거스름돈 (0) | 2021.02.23 |
|---|---|
| 백준 9095 번 : 1, 2, 3 더하기 (0) | 2021.02.23 |
| 백준 11726번 : 2*n 타일링 (0) | 2021.02.18 |
| 백준 9625번 : BABBA (0) | 2021.02.18 |
| 백준 11721번 : 열 개씩 끊어 출력하기 (0) | 2021.02.17 |



